计算机组成原理——进制与编码
BCD码
对于计算机来讲二进制方便计算机处理,而对于人类来讲十进制符合人类使用习惯。
二进制转换成十进制需要按以下方式:
$$ K_nr^n+K_{n-1}r^{n-1}+...+K_1r^1+K_0r^0 $$
由此可见转换相当麻烦。
8421码
为了快速变换就需要一种二进制编码的方式(Binary-Coded Decimal)实现二进制与十进制一一对应,其中一种方式为8421码,其映射方式如下。
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|
| 0000 | 0001 | 0010 | 0011 | 0100 | 0101 | 0110 | 0111 | 1000 | 1001 |
对于十进制5+8这种操作,计算机会将0101和1000交给算术逻辑运算单元进行加法运算。但是运算结果为1101不在映射表里。
为了让运算结果符合映射规则,会对1010到1111这个区间的数,也就是10到15之间的数再加一个6,这样最高位必然向前进1,则剩下的部分就落在这个映射表中了。
例如对于13这个结果,二进制表示为1101,加6就成了00010011,而0011正好对应3,0001对应1。
当然对于人手算来讲,只需要写出十进制13,然后把每一位十进制对应的8421码的方式拼接即可。即1对应0001,而 3对应0011,拼接起来就是00010011,来表示13的8421编码方式。
余3码
余3码是在8421的基础上再加上3,于是存在以下映射关系:
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|
| 0011 | 0100 | 0101 | 0110 | 0111 | 1000 | 1001 | 1010 | 1011 | 1100 |
8421码每个二进制位的权值都是固定不变的,都是8,4,2,1。而对于余3码每一位的权值不是固定的。因此8421这种也被称为有权码,而余3码这种类型的被称为无权码。
2421码
2421码是有权码,对应权值分别为2,4,2,1,其映射关系如下:
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|
| 0000 | 0001 | 0010 | 0011 | 0100 | 1011 | 1100 | 1101 | 1110 | 1111 |
可以看到,对于5到9的数都是以1开头。这是因为如果按照2421编码方式5可以表示为0101也可以表示为1011,为了避免歧义就采用了这种规定。
无符号整数
无符号整数,即从零开始的整数,0,1,2,3,...
在C语言中,只需要用unsigned这个关键字即可生命一个无符号类型的数字。
unsigned short a=1; //无符号短整型,2Byte
unsigned int b=2; //无符号整型,4Byte我们这里主要关心无符号整数在计算机内的运算以及硬件实现。
若一个机器字长为8位(现在的计算机通常是32位或64位),其寄存器只能存8位,也就是说无符号整数二进制位数是有上限的。
对于真值0,其二进制表示也是0,但是在8位寄存器中要扩展成8位00000000。、
对于8位寄存器存放的真值只能是0到255,总共256个数。如果真值256转换成二进制存放进去的话,会发生溢出现象,也就是说最高位会被忽略掉只能存放低8位,最终寄存器里的二进制为00000000。
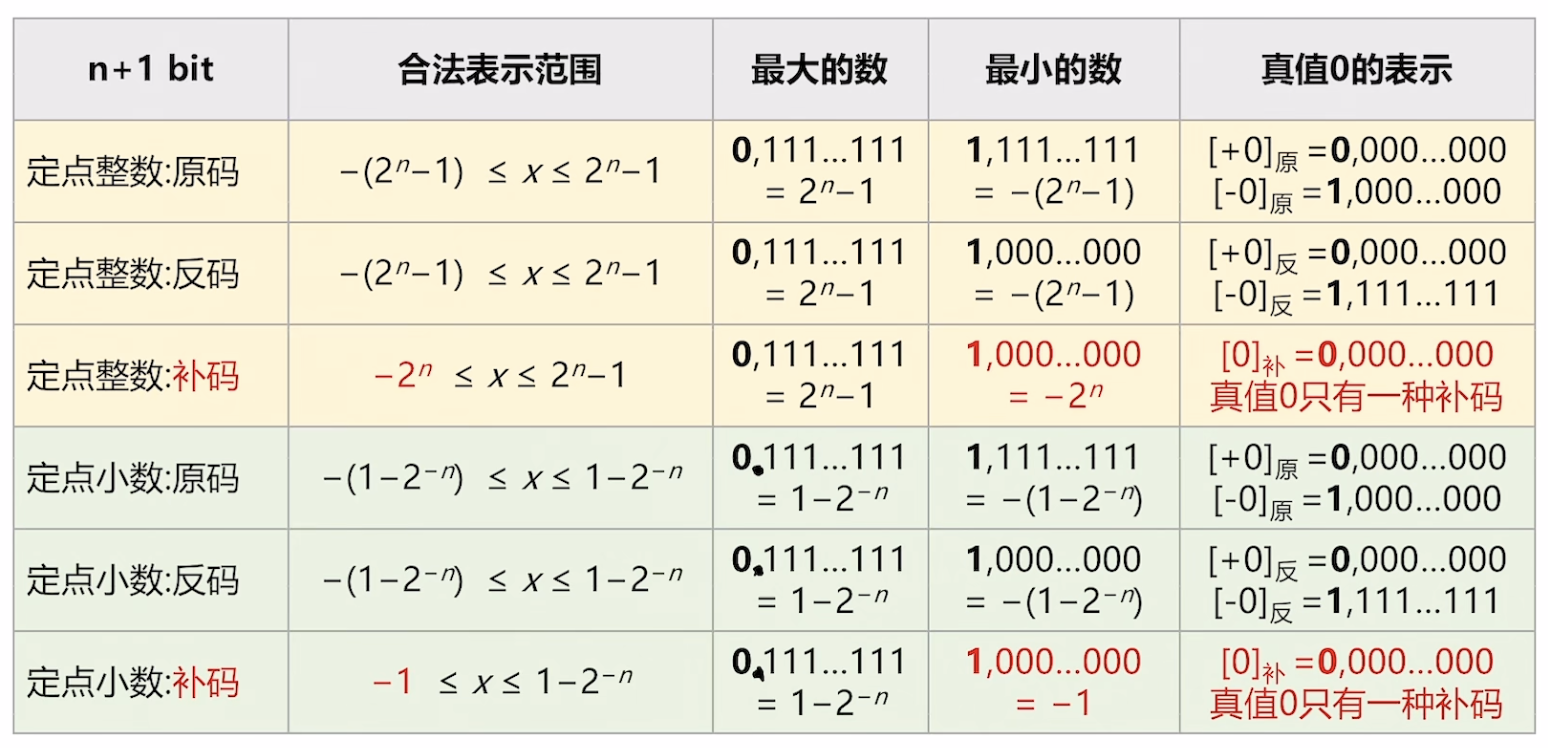
由此可见n bit无符号整数可以表示的范围为$0$到$2^{n}-1$,最小的数每一二进制位全为0,最大的数全为1。
加法
接下来我们看下在计算机中,无符号整型的加法是如何实现的。我们以99+9为例,它们的8比特二进制分别为01100011与00001001。它们相加只需要从最低位开始,并向着更高位进位即可,因此结果为01101100。
当然两个无符号整型相加在8bit的限制下可能存在溢出的情况,例如255+1,只需要将结果保留低8位即可。
减法
在计算机中无符号整型减法需要遵循以下步骤:
- 被减数不变,减数全部按位区反,末为全部加1,减法变加法
- 从最低位开始,按位相加,并往更高位进位
加法电路造价更贵,而减法电路更昂贵,因此将减法转换成加法更节省成本。
我们以99-9为例,其二进制8比特表示分别为01100011和00001001,按上述算法,需要对减数取反为11110110,并且末尾加1,变成了11110111。
然后我们只需要将01100011和11110111按照加法的方式进行相加即可得到90的二进制01011010。
带符号整数
在数学里整数的概念即为带符号整数,如-1,-2,0,3,4等。
在C语言中我们可以用以下方式来表示带符号整数:
short a = 1; //带符号整数,短整型,2Byte
int b = -2; //带符号整数,整型,4Byte原码表示法
原码表示法最高位为符号为,最高位若为0,则为正数;若最高位为1,则为负数。剩下的较低的二进制位表示其数值。
也就是说,带符号的整数,若寄存器为n+1位,则可以表示的范围是$-(2^n-1)$到$2^n-1$。对于真值0有两种形式,一种是+0,另一种是-0,前者包括符号位在内的每一位都是0,后者除了符号位为1外,其他位都是0。
原码表示带符号整数,缺点是符号位不能参与运算,因此需要设计更复杂的硬件电路才能处理,成本比较高。
补码表示法
补码的转换
为了使符号位能够参与运算,于是就设计了补码表示法。
对于正整数来说,其补码与反码一致,不做改变。
而对于负整数来说,遵循以下原则:
- 原码符号位不变,数值位按位取反,得到反码
- 反码末位加1,得到补码
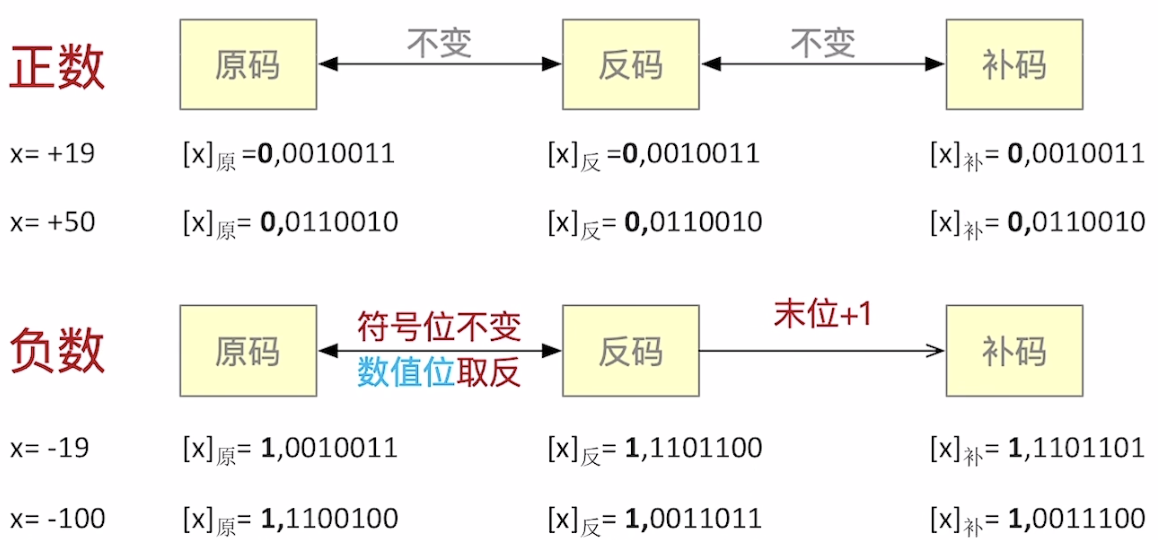
当然对于手算,则有更简单的方式。正数原码与补码之间的转换依然保持不变,而对于负数,只需要将原码从右往左找到第一个1,然后这个1与符号位之间的二进制位(不包括符号位与这个第一个1)全部取反即为补码。同理对于负数补码,我们也是从右往左找到第一个1,然后这个1与符号位之间的二进制位(不包括符号位与这个第一个1)全部取反即为原码。
我们以-100为例,其补码如下:
$$ 1\space0011100 $$
我们找到从右往左第一个1
$$ 1\space 0011\space100 $$
然后对中间的二进制位取反,即得到-100的原码
$$ 1 \space 1100 \space 100 $$
反之依然成立。
对于反码,真值0的表示方式同样分为+0和-0,前者所有位全为0,后者所有位全为1。
而对于补码,真值0的表示方式只有一种,那就是所有的二进制位都是0。
在计算机中有符号整数通常是以补码的形式存在的。
补码加法
我们以19+(-19)为例,19的补码为00010011,-19的补码为11101101,二者相加只需要从最低位开始,进行二进制加法,向更高位进位即可,结果为00000000。
使用补码相加就使得符号位参与了运算,还能得到正确的结果。
补码减法
对于补码减法运算,我们仍旧按照之前的思想,将其转换为加法运算。对于A-B,实际上可以写成A+(-B),也就是说,我们只需要将减数的符号为取反,然后按照补码加法原则进行计算即可。
移码
移码只需要在补码的基础上取反符号为即可。但是移码只能表示整数,而补码和原码可以表示小数。
由于补码的真值0表示方式只有一种,那么移码的真值0表示方式也是只有一种,那就是符号位为1,其他二进制位为0。
总结

定点小数
定点小数的小数点位置是固定的。我们之前所说的带符号整数,其实也可以叫做定点整数,因为其小数点实际上是隐含的。
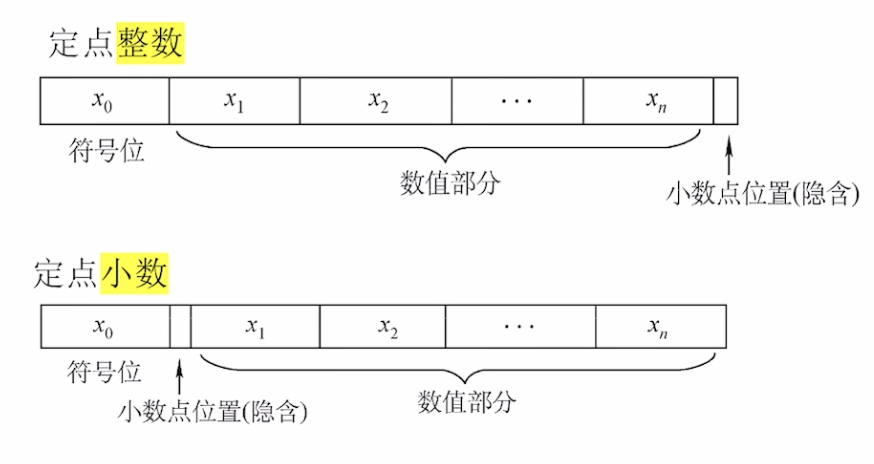
我们之前在带符号整数的移码部分提到过,带符号整数可以用原码、反码、补码、移码来表示,而定点小数的表示方式只有原码、反码、补码。
原码表示
定点小数同样有一个符号位,若为1则代表负数,若为0则代表整数。
对于定点小数,其小数位之后的第i位(i>0)的权值为$2^{-i}$
我们假设定点小数的小数点位置在符号为之后,计算机字长为8位,则其每一位的权值如下图所示:

反码、补码
定点小数的反码、补码计算方式同带符号整数,这里不过多叙述。
定点小数加法、减法
定点小数采用补码加法,其算法同带符号整数。此外补码减法也同带符号整数。
定点小数与定点整数的对比
定点小数与定点整数位数扩展是不一样的,对于定点小数来讲,位数扩展的位数是在最低位之后;而对于定点整数,位数扩展是在符号位与数值位之间。
我们分别对4bit的二进制定点小数1.110与定点整数1,110分别扩充4位。(注意这里的小数点和逗号只是用于分割表示,看起来更直观一点,实际上其二进制并没有小数点和逗号)
定点小数扩展后其二进制
$$ 1.1100000 $$
而对于定点整数扩充后其二进制为
$$ 1,0000110 $$
奇偶校验码
校验位
假设A、B两台计算机进行通信,其信息编码方式如下
| A | B | C | D |
|---|---|---|---|
| 00 | 01 | 10 | 11 |
但是由于信道的电气特性引起信号幅度、频率、相位的畸变,信号反射、串扰、闪电、大功率电机的启停等,都有可能造成传输链路的数据信号产生差错,因此我们可以增加一个二进制位,来判断数据传输是否发生差错。
| A | B | C | D |
|---|---|---|---|
| 100 | 001 | 010 | 111 |
3bit映射到4个合法状态,有4个冗余的非法状态。
我们假设A传输数据001,但是到经过物理链路之后,B收到的信息为000的非法状态,B就可以判断出两者之间传输的数据发生错误。
奇偶校验
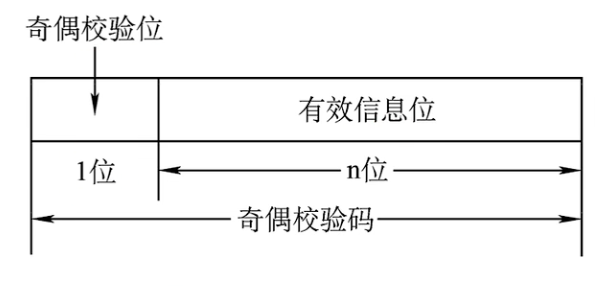
若存在有效信息位为n位,我们只需在头部或者尾部添加1个奇偶校验位来判断信息是否有误即可。
奇校验码:整个校验码中(有效信息和校验位)中1的个数为奇数。
偶校验码:整个校验码中(有效信息和校验位)中1的个数为偶数。
我们来看一个例子,给出两个编码1001101和1010111的奇校验码和偶校验码。假设最高位为校验位,其余7位为信息位,则对应的奇偶校验码如下:
- 奇校验码分别是
1 1001101、0 1010111。前者由于信息位中1的个数是4个即偶数个,所以最高位也就是校验位需要补一个1才能让整个校验码的1为奇数个;同样,后者信息位中1度个数为5个,为奇数个,所以最高的校验位不需要补1,填写0即可。 - 偶检验码分别是
0 1001101、1 1010111。由于是写偶校验码,前者信息位中1的个数为4个即偶数个,因此最高位即校验位不用补充1,填0即可;而后者信息位中的1的个数为5个即奇数个,因此最高位填1,使整个校验码中的1的个数达到偶数个。
奇偶校验码有一定局限性。假设我们采取偶校验码1 1010111,假如在信息传输过程中最低两位的1都变成了0,接收方收到校验码后是检查不出错误的,因为校验码中的1仍为偶数个。
硬件实现
偶校验的硬件实现
对信息位中的每一位进行异或运算(模2加运算)。异或运算的法则如下:
| 0异或0 | 0异或1 | 1异或0 | 1异或1 |
|---|---|---|---|
| 0 | 1 | 1 | 0 |
即异或运算两个比特不同才为1,相同为0。
对于信息位1001101我们可以通过运算得到偶校验位为0
$$ 1 \oplus 0 \oplus 0 \oplus 1 \oplus 1 \oplus 0 \oplus 1 = 0 $$
奇校验的硬件实现
我们通过上面的知识可以知道,若信息位中有偶数个1,偶校验位为0,若有奇数个1则偶校验位是1。
那么对于奇校验位,只需要按照偶校验位那样进行异或运算,然后对最终结果取非即可。也就是说如果异或运算结果为0,我们就让奇校验位为1;若异或运算结果为1,则奇校验位就是0。
