扫描转换椭圆与圆的绘制

前提

我们先来设计一种数据类型

class Point{
public:
  double x,y;
  Point(){this->x = 0; this->y = 0;}
  Point(double x, double y){this->x=x;this->y=y;}
};

注意此处的类型为double这一点很重要，因为在某些迭代过程中设置为int会导致坐标数值不变，然后进入死循环或者绘制不出来。如果需要int类型，那么无需担心，double到int之间会有一个隐式转换，直接将Point类型中属性值赋给对应的变量即可。（如果你想知道哪些情况下使用int会无法绘制请参考椭圆部分的DDA算法）

圆

基础知识

在直角坐标系中，圆心在原点上的圆有如下方程：

$$ x^2+y^2 = R^2 $$

其中R为圆的半径。

若圆心不在原点上，则有更一般形式的方程。

假设圆心为(a,b)则圆的方程为：

$$ (x-a)^2+(y-b)^2 = R^2 $$

同样的，对于圆心在原点上的圆我们有参数方程：

$$ \begin{cases} x=R\cos \theta \\ y = R\sin \theta \end{cases} $$

对于圆心不在原点上的圆有参数方程：

$$ \begin{cases} x=a+R\cos \theta \\ y = b+R\sin \theta \end{cases} $$

将$\theta$离散化可得

$$ \theta = 2\pi \frac{i}{n},i\in[0,n] $$

然而我们在计算的时候并不喜欢圆心不在原点上的圆，所以在进行扫描转换之前，我们先平移坐标系原点至圆心，当扫描转换完成后再平移回去。故而在接下来的讨论中，我们只使用圆心在原点上的方程。

此外，圆还有如下几种对称性质：

• 关于 $y=\pm x$ 对称
• 关于x轴对称
• 关于y轴对称

这几条对称轴将圆分割成了八等份，也就是说，给出圆周上任意一个点，就能通过数学计算得到其余的7个点。这对于圆的绘制就简单了许多，我们只需要计算出八分之一的圆弧，就能得到整个圆。

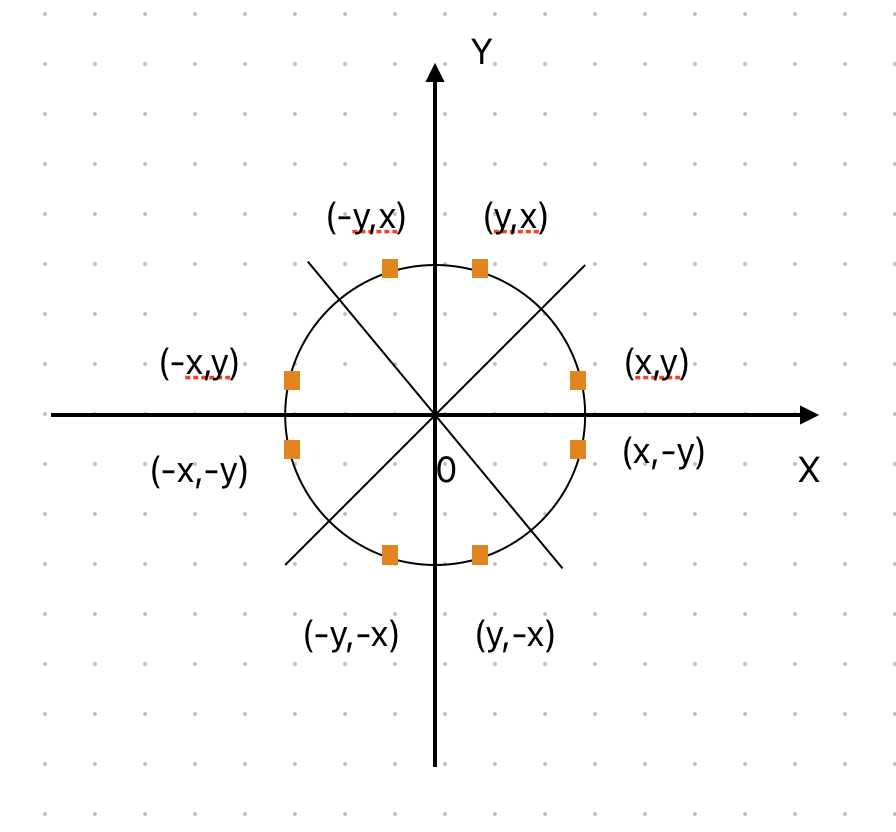
在开始之前我们不妨约定这样一个函数（C++风格伪代码，实际代码根据你自己的API来调用相应的函数）

/* 以原点为圆心，通过八分之一圆上的一点绘制其余七个对称点
 * p为绘制的点
 * center为圆心
 * color为绘制颜色
 */
void
draw_circle_point(const Point& p, 
                  const Point& center,
                  Color color){
  int x = p.x;
  int y = p.y;
  int ox = center.x, oy = center.y;
  
  setPixel(x+ox,y+oy,color);    //绘制像素
  setPixel(y+ox,x+oy,color);
  setPixel(-y+ox,x+oy,color);
  setPixel(-x+ox,y+oy,color);
  setPixel(-x+ox,-y+oy,color);
  setPixel(-y+ox,-x+oy,color);
  setPixel(y+ox,-x+oy,color);
  setPixel(x+ox,-y+oy,color);
}

此外在接下来的计算中可能会用到三角函数的和差公式，请牢记这一点：

$$ \sin{(\alpha \pm \beta)}=\sin{\alpha}\cos{\beta}\pm \cos{\alpha}\sin{\beta} \\ \cos{(\alpha \pm \beta)} = \cos{\alpha}\cos{\beta} \mp \sin{\alpha}\sin{\beta} $$

直接计算法

直接生成有两种方式，一种是根据直角坐标系下笛卡尔方程来计算，另一种根据参数方程。

笛卡尔方程直接计算

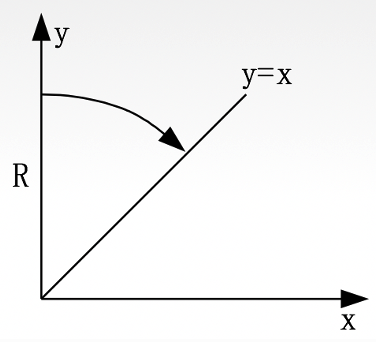
我们扫描这样圆弧上的点。

根据方程 $x^2+y^2=R$ 可以得到：

$$ \begin{cases} x_{i+1} = x_i+1,x\in [0,\frac{R}{\sqrt{2}}] \\ \\ y_{i+1} = round(\sqrt{R^2-x_{i+1}^2}) & \end{cases} $$

故有C++风格伪代码

const double SQRT_2 = sqrt(2);

/*
 * 利用笛卡尔方程直接绘制圆
 * circle_center为圆心
 * R为圆半径
 * color为绘制的颜色
 */
void 
draw_circle_common(const Point& circle_center, 
                   double R, 
                   Color color){
  double xr = R/SQRT_2;
  Point p;
  for(p.x=0;p.x<=xr;p.x++){
    p.y=sqrt(R*R-p.x*p.x);
    draw_circle_point(p, circle_center, color);
  }
}

参数方程直接计算

我们是根据离散化的参数方程来计算的

$$ \begin{cases} x=R\cos (2\pi \frac{i}{n}) \\ y = R\sin (2\pi \frac{i}{n}) \end{cases} $$

C++风格伪代码如下

const double PI = 4.0*atan(1.0);    //圆周率

/*
 * 利用参数方程直接绘制圆
 * circle_center为圆心
 * R为圆半径
 * color为绘制的颜色
 * n为离散化程度，n越大越精细但越耗时
 */
void 
draw_circle_param(const Point& circle_center, 
                   double R, 
                   Color color,int n){
  int k;
  Point p;
  for(k=0;k<=n;k++){
    p.x = R*cos(2*PI*k/n);
    p.y = R*sin(2*PI*k/n);
    draw_circle_point(p, circle_center, color);
  }
  
}

DDA算法

数值微分算法(Digital Differential Analyzer, DDA)在前面绘制直线的文章中已经提到过了，现在我们来尝试使用它绘制圆。

我们考虑如下图

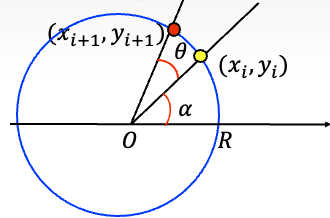
$$ \begin{cases} x_i=R\cos \alpha \\ y_i = R\sin \alpha \end{cases} $$

我们让当前角度 $\alpha$ 沿着逆时针方向加上几个极小的角度量 $\theta$

就得到了下一个点

$$ (x_{i+1},y_{i+1}) = (R\cos{(\alpha+\theta)},\space R\sin{(\alpha + \theta)}) $$

所以，对于x有如下递推式

$$ x_{i+1} = R\cos{(\alpha+\theta)} = R\cos\alpha\cos\theta - R\sin\alpha\sin\theta = x_i\cos\theta-y_i\sin\theta $$

同样对于y也有如下递推式

$$ y_{i+1} = R\cos{(\alpha + \theta)} = y_i\cos\theta+x_i\sin\theta $$

又因为当 $\theta$ 足够小的时候有

$$ \cos\theta \approx 1\\ \sin\theta \approx \theta $$

故递推式可以改写为

$$ \begin{cases} x_{i+1} = x_i - y_i\theta \\ y_{i+1} = y_i+x_i\theta \end{cases} $$

知道这一点我们可以写出C++风格伪代码：

/*
 * DDA画圆
 * circle_center为圆心
 * R为圆半径
 * color为绘制的颜色
 */
void 
draw_circle_dda(const Point& circle_center,
                double R,
                Color color){
  Point p;
  p.x = R;
  p.y = 0;
  int x_old;
  double delta=1.0/R, theta=0;
  for(theta=0; theta<=PI/4; theta+=delta){
    draw_circle_point(p, circle_center, color);
    x_old = p.x;
    p.x -= p.y*delta;
    p.y += x_old*delta;
  }
  
}

中点Bresenham算法

基本思路

圆的隐式方程如下

$$ x^2 + y^2 - R^2 = 0 $$

由此构造二元函数

$$ F(x,y) = x^2 + y^2 -R^2 $$

然后根据这个函数来判别点与圆的位置关系：

• 若 $F(x,y)=0$ ，则点在圆上
• 若 $F(x,y)>0$ ，则点在圆外
• 若 $F(x,y)<0$ ， 则点在圆内

我们考虑如下圆弧

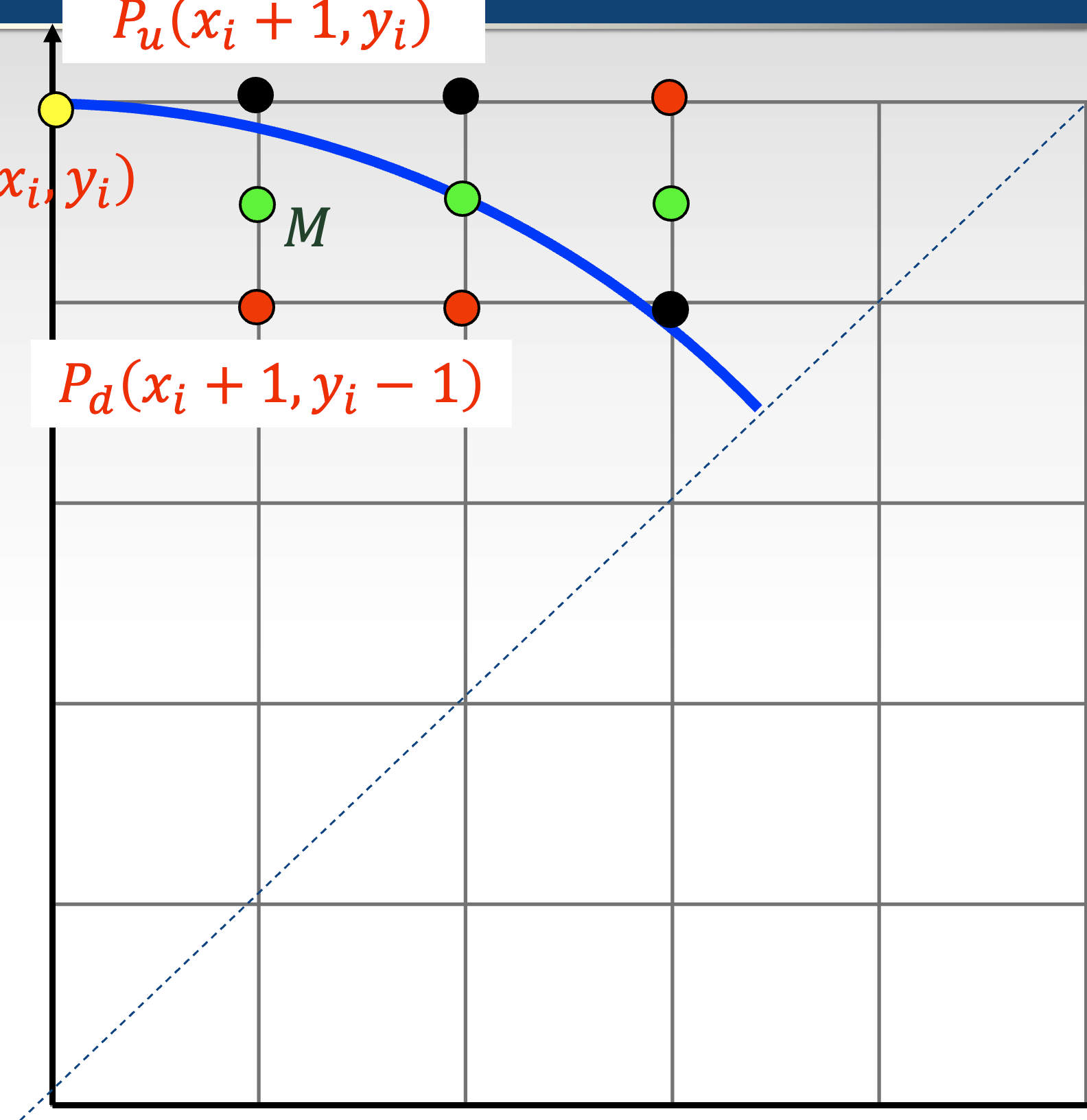
对于点$(x_i,y_i)$，有下一可选择两点中点坐标 $(x_M,y_M)$有：

• 当 $F(x_M,y_M)<0$ 时，取点 $(x_i+1,y_i)$
• 当 $F(x_M,y_M)>0$ 时，取点 $(x_i+1,y_i-1)$
• 当 $F(x_M,y_M)=0$ 时，约定取点 $(x_i+1,y_i)$

构造判别式

$$ d_i = F(x_M,y_M) = (x_i+1)^2 + (y_i-0.5)^2 - R^2 $$

当 $d_i \le 0$的时候，下一中点坐标为

$$ (x_i + 2, y_i-0.5) $$

得到递推式

$$ d_{i+1} = F(x_i+2,y_i-0.5)=d_i+2x_i+3 $$

同理对于 $d_i>0$ 的时候有下一中点

$$ (x_i+1,y_i-1) $$

递推式如下：

$$ d_{i+1} = F(x_i+1,y_i-1)=d_i+2(x_i-y_i)+5 $$

我们还得求出第一次迭代时候的初始值 $d_0$

$$ d_0 = F(1,R-0.5) = 1.25-R $$

综上所述

$$ d_{i+1} = \begin{cases} d_i+2x_i+3, &d_i\le 0 \\ d_i+2(x_i-y_i) + 5, &d_i>0 \end{cases} $$

$$ d_0 = 1.25-R $$

代码如下（当然还是伪代码）：

/*
 * 中点Bresenham画圆
 * circle_center为圆心
 * R为圆半径
 * color为绘制的颜色
 */
void
draw_circle_midb(const Point& circle_center,
                double R,
                Color color){
  Point p;
  p.x = 0, p.y = R;
  double d = 1.25-R;
  while(p.x<=p.y){
    draw_circle_point(p, circle_center, color);
      if(d<=0)
          d+=2*p.x+3;
    else{
      d += 2*(p.x-p.y)+5;
      p.y--;
    }
    
    p.x++;
  }
  
}
  

改进

在计算中仍有小数运算，为了避免这种情况令 $d-0.25$ 代替原来的 $d$

由于为int类型，$d\le -0.25$ 可认为是 $d\le 0$

$$ d_{i+1} = \begin{cases} d_i+2x_i+3, &d_i\le 0 \\ d_i+2(x_i-y_i) + 5, &d_i>0 \end{cases} $$

$$ d_0 = 1-R $$

代码就变成了（其实改动不是很大）

/*
 * 改进中点Bresenham画圆
 * circle_center为圆心
 * R为圆半径
 * color为绘制的颜色
 */
void
draw_circle_midb(const Point& circle_center,
                double R,
                Color color){
  Point p;
  p.x = 0, p.y = R;
  int d = 1-R;
  while(p.x<=p.y){
    draw_circle_point(p, circle_center, color);
      if(d<=0)
          d+=2*p.x+3;
    else{
      d += 2*(p.x-p.y)+5;
      p.y--;
    }
    
    p.x++;
  }
  
}

椭圆

基础知识

椭圆方程为

$$ \frac{x^2}{a^2}+\frac{y^2}{b^2} = 1, (a>0,b>0,a\ne b) $$

隐式方程为

$$ b^2x^2 + a^2y^2 -a^2b^2 = 0 $$

注意我们为了统一表示长轴在y上和长轴在x轴上的椭圆，并没有指明 $a>b$ 还是 $b>a$ 。

有参数方程：

$$ \begin{cases} x = a\cos\theta \\ y = b\cos\theta \end{cases} $$

我们只考虑中心在原点的椭圆，如果不在原点先平移坐标系，扫描转换后再平移回去。

对于中心在原点的椭圆有如下对称性质：

• 关于x轴对称
• 关于y轴对称

故我们用四分法来绘制椭圆。

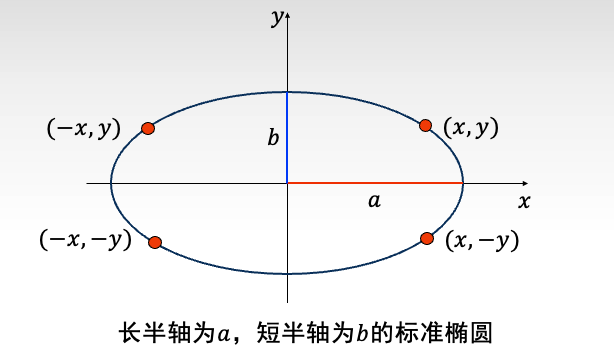
也就是说我们只需有四分之一的弧线，即可绘制出整个椭圆。

不妨约定一个函数

/* 以原点为中心，通过四分之一弧线上的一点绘制其余四个对称点
 * p为绘制的点
 * center为椭圆中心
 * color为绘制颜色
 */
void
draw_oval_point(const Point& p, 
          const Point& center,
          Color color){
  int x = p.x;
  int y = p.y;
  int ox = center.x, oy = center.y;
  
  setPixel(x+ox,y+oy,color);    //绘制像素
  setPixel(-x+ox,y+oy,color);
  setPixel(-x+ox,-y+oy,color);
  setPixel(x+ox,-y+oy,color);
}

直接计算法

笛卡尔方程

$$ x_{i+1} = x_i+1 \\ y_{i+1} = round(\sqrt{\frac{a^2b^2-b^2x_{i+1}^2}{a^2}}) $$

代码如下

/*
 * 利用笛卡尔方程直接绘制椭圆
 * center为中心点
 * a为标准方程x分数线下的参数（此处不一定为长轴长度一般，也可能是短轴长一半）
 * b为标准方程下y分数线下的参数（同理不一定为短轴长一半）
 * color 为颜色
 */
void
draw_oval_common(const Point& center, 
                 double a, 
                 double b,
                 Color color){
  double aa = a*a;
  double bb = b*b;
  double temp = aa*bb;
  Point p;
  for(p.x=0;p.x<=a;p.x++){
    p.y = sqrt((temp-bb*p.x*p.x)/aa);
    draw_oval_point(p,center,color);
  }
}

参数方程

离散化参数方程

$$ \begin{cases} x=a\cos (2\pi \frac{i}{n}) \\ y = b\sin (2\pi \frac{i}{n}) \end{cases} $$

代码如下：

/*
 * 利用参数方程直接绘制椭圆
 * center为中心点
 * a为标准方程x分数线下的参数（此处不一定为长轴长度一般，也可能是短轴长一半）
 * b为标准方程下y分数线下的参数（同理不一定为短轴长一半）
 * color 为颜色
 * n为分割参数，越大越精细但越慢
 */
void 
draw_oval_param(const Point& center, 
                   double a,
                   double b,
                   Color color,int n){
  int k;
  Point p;
  for(k=0;k<=n;k++){
    p.x = a*cos(2*PI*k/n);
    p.y = b*sin(2*PI*k/n);
    draw_oval_point(p, center, color);
  }
  
}

DDA算法

$$ x_{i+1} = a\cos{(\alpha + \theta)} =a\cos\alpha\cos\theta - a\sin\alpha\sin\theta = x_i\cos\theta-\frac{a}{b}y_i\sin\theta \\ y_{i+1} = b\cos{(\alpha + \theta)} = y_i\cos\theta+\frac{b}{a}x_i\sin\theta $$

当 $\theta$ 足够小的时候可认为

$$ \cos\theta \approx 1\\ \sin\theta \approx \theta $$

即有

$$ \begin{cases} x_{i+1} = x_i - \frac{a}{b} y_i\theta \\ y_{i+1} = y_i+\frac{b}{a} x_i\theta \end{cases} $$

/*
 * DDA绘制椭圆
 * center为中心点
 * a为标准方程x分数线下的参数（此处不一定为长轴长度一般，也可能是短轴长一半）
 * b为标准方程下y分数线下的参数（同理不一定为短轴长一半）
 * color 为颜色
 */
void 
draw_circle_dda(const Point& center,
                double a,
                double b,
                Color color){
  Point p;
    p.x = a;
  p.y = 0;
  double d = 1/a;
  for(double t=0;t<=PI/2;t+=d){
    draw_oval_point(p,center,color);
    double old_x = p.x;
    p.x -= p.y/b;
    p.y += old_x*b/(a*a);
  }
  
}

中点Bresenham算法

算法原理

• 从 $(0,b)$ 到 $(a,0)$ 逆时针地确定最佳逼近于第一象限的椭圆弧像素序列
• 记切线斜率为 $k$ 。在上半部分， $-1\le k \le0$ ，最大位移方向为x；在下半部分， $k\le-1$ ，最大位移方向为y。
• 分别对这两部分判断中点与椭圆的关系

我们先来看第一象限的上半部分

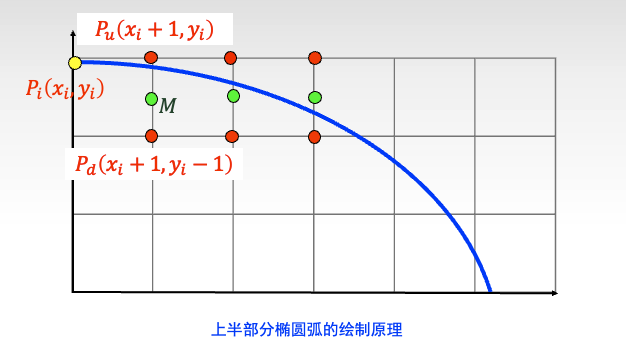
与圆同理，判别式为：

$$ d_i = F(x_M,y_M) = b^2(x_i+1)+a^2(y_i-0.5)^2 - a^2b^2 $$

• 若 $d_i\le 0$ ，取 $(x_i+1,y_i)$
• 若 $d_i>0$， 取 $(x_i+1,y_i-1)$

当 $d_i \le 0$ 的时候，下一中点为 $(x_i+2,y_i-0.5)$ ，有递推式：

$$ d_{i+1} = F(x_i+2,y_i-0.5) = d_i + b^2(2x_i + 3) $$

当 $d_i>0$ 的时候，下一中点为 $(x_i-2,y_i-1.5)$ ，有递推式：

$$ d_{i+1} = d_i + b^2(2x_i+3)+a^2(-2y_i+2) $$

初始值为

$$ d_0 = b^2+a^2(-b+0.25) $$

然后再来看看下半部分

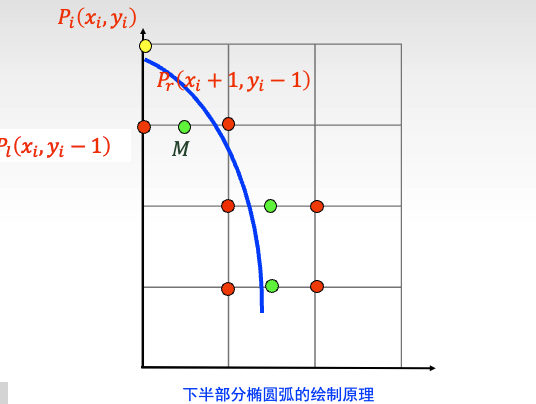
同样有判别式

$$ d_i = b^2(x_i+0.5)^2+a^2(y_i-1)^2-a^2b^2 $$

当$d_i\le 0$ 时，取点 $(x_i+1,y_i-1)$ 且有下一中点 $(x_i+1.5, y_i-2)$

$$ d_{i+1} = d_i+b^2(2x_i+2)+a^2(-2y_i+3) $$

当 $d_i>0$ 时，取 $(x_i,y_i-1)$ ，有下一中点 $(x_i+0.5,y_i-2)$

$$ d_{i+1} = d_i + a^2(-2y_i+3) $$

但初始值如何计算？

既然无法直接得到，我们干脆利用上半部分最后一个点来计算下半部分初始值！

$$ d_0 = b^2(x+0.5)^2+a^2(y-1)^2-a^2b^2 $$

代码

void
draw_oval_midb(const Point& center, double a, double b, Color color){
  Point p;
  double d1 = b*b+a*a*(-b+0.25);
  p.x = 0;
  p.y = b;
  draw_oval_point(p,center,color);
  
  
  while(b*b*(p.x+1)<a*a*(p.y-0.5)){
    if(d1<0){
      d1+=b*b*(2*p.x+3);
      p.x++;
    }else{
      d1+=b*b*(2*p.x+3)+a*a*(-2*p.y+2);
      p.x++;p.y--;
    }
    draw_oval_point(p,center,color);
  }
  
  //下半部分
  double d2 = sqrt(b*(p.x+0.5))+a*(p.y-1)-a*b;
  while(p.y>0){
    if(d2<0){
      d2 += b*b*(2*p.x+2)+a*a*(-2*p.y+3);
      p.x++;p.y--;
    }else{
      d2+=a*a*(-2*p.y+3);
      p.y--;
    }
    
    draw_oval_point(p,center,color);
  }
  
  
}

结束

终于写完了，累死我了。尤其是椭圆那里，程序怎么都不过，后来才发现公式推导推错了，又把推到过程重新敲了一遍。

什么你问我写的明明是伪代码，为什么还能跑。很简单，因为本来我的代码就是仿照一些接口写的，有部分甚至直接粘贴就能运行，不能运行的改个函数名加个头文件就能跑。

以下就是我在Qt中的部分测试代码，代码几乎一致，顶多加几个对象

#include "mainwindow.h"
#include "./ui_mainwindow.h"
#include <qmath.h>
#include <QPainter>

const double PI = 4*atan(1.0);


MainWindow::MainWindow(QWidget *parent)
    : QMainWindow(parent)
    , ui(new Ui::MainWindow)
{
    ui->setupUi(this);
}

void MainWindow::draw_oval_point(const Point &p, const Point &center){
    int x = p.x;
    int y = p.y;
    int ox = center.x;
    int oy = center.y;


    this->image->setPixel(x+ox,y+oy,qRgb(255,0,0));
    this->image->setPixel(-x+ox,y+oy,qRgb(255,0,0));
    this->image->setPixel(x+ox,-y+oy,qRgb(255,0,0));
    this->image->setPixel(-x+ox,-y+oy,qRgb(255,0,0));
}


void MainWindow::draw_oval_dda(const Point& center,double a,double b){
    Point p;
    double d1 = b*b+a*a*(-b+0.25);
    p.x = 0;
    p.y = b;
    draw_oval_point(p,center);


    while(b*b*(p.x+1)<a*a*(p.y-0.5)){
        if(d1<0){
            d1+=b*b*(2*p.x+3);
            p.x++;
        }else{
            d1+=b*b*(2*p.x+3)+a*a*(-2*p.y+2);
            p.x++;p.y--;
        }
        draw_oval_point(p,center);
    }


    //下半部分
    double d2 = sqrt(b*(p.x+0.5))+a*(p.y-1)-a*b;
    while(p.y>0){
        if(d2<0){
            d2 += b*b*(2*p.x+2)+a*a*(-2*p.y+3);
            p.x++;p.y--;
        }else{
            d2+=a*a*(-2*p.y+3);
            p.y--;
        }

        draw_oval_point(p,center);
    }
}

void MainWindow::paintEvent(QPaintEvent *event){
    QPainter painter(this);
    this->image = new QImage(1000, 600, QImage::Format_RGB32);
    this->image->fill(Qt::white);
    Point center(400,200);

    this->draw_oval_dda(center,300,100);
    painter.drawImage(QPoint(0, 0), *image);

}

MainWindow::~MainWindow()
{
    delete image;
    delete ui;
}

如果你发现文章中有逻辑错误，请在下方留言，与圆有关的部分代码我没有测试。