计算机组成原理——指令系统

指令概念

指令是指计算机执行某种操作的命令，是计算机运行的最小功能单位。一台计算机的所有指令的集合构成该计算机的指令系统，也称为指令集。

一台计算机只能够执行自己的指令集中的指令，通常不能执行其他架构的指令。如ARM的机器只能执行ARM指令集的指令，而不能执行X86架构指令集的指令，但是一些工程师会设计一些转译器，将X86的某些程序翻译成ARM指令的，从而实现在ARM机器上跑X86应用程序。

指令格式

一条指令就是机器语言的一个语句，它是一组有意义的二进制代码。一条指令通常包括操作码OP和地址码A两个部分。

操作码指明了用户要干什么，例如停机中断、加减乘除等；地址码指明了对谁进行操作。

一条指令可能包含多个地址码，根据地址码数目不同，可以分为零地址指令、一地址指令、二地址指令……

如果机器的指令长度固定不变，那么地址码数量越多，寻址能力就越差。

n位地址码寻址范围$2^n$

按地址数目分类

零地址指令

零地址指令不需要给出地址码。

通常有以下两种情况需要用零地址指令：

• 不需要操作数，如空操作、停机、关中断等指令。
• 堆栈计算机，两个操作数隐含存放在栈顶和次栈顶，计算结果压回栈顶。

一地址指令

一地址指令需要一个地址码。

通常以下情况用到这种指令：

• 只需要单操作数，如加1、减1

$$ OP(A_1)\to A_1 $$

• 需要两个操作数，单其中一个隐含在寄存器中（如隐含在ACC）

$$ (ACC)OP(A_1)\to ACC $$

$A_1$指某个主存地址，$(A_1)$表示存放的内容，下标表示操作码后跟的第1个地址码。

二地址指令

二地址指令后根两个地址码，第一个地址码$A_1$为目的操作数，第二个地址码为源操作数$A_2$。

二地址指令常用于需要两个操作数的算术运算、逻辑运算相关指令。

$$ (A_1)OP(A_2)\to A_1 $$

完成一条指令需要4次访存，分别为取指、读$A_1$、读$A_2$、写$A_1$

三地址指令

常用于需要两个操作数的算术运算、逻辑运算相关的指令，通常第三个操作码为结果存放的地址。

$$ (A_1)OP(A_2)\to A_3 $$

完成一条指令需要4次访存，分别为取指、读$A_1$、读$A_2$、写$A_3$

四地址指令

四地址指令在三地址指令的基础上多了一个存放下一条指令地址的地址码，通常是第四个地址码。

$$ (A_1)OP(A_2)\to A_3,A_4=next $$

完成一条指令需要4次访存，分别为取指、读$A_1$、读$A_2$、写$A_3$

正常情况下，取指令之后程序计数器（缩写PC，下同）加1，指向下一条指令，而采用四地址指令，在执行指令后将PC的值修改为$A_4$所指地址。

按指令长度分类

指令字长：一条指令的总长度（可能会变）

机器字长：CPU进行一次整数运算所能处理的二进制数据的位数（通常与ALU直接相关）

存储字长：一个存储单元中二进制代码的位数（通常与MDR位数相同）

半字长指令、单字长指令、双字长指令等概念都是指指令长度是机器字长的多少倍。

假设机器字长与存储字长都是16bit，那么取一条双字长指令（32bit）需要2次访存。

若指令系统中所有指令长度都相等，则称为定长指令字结构，若指令长度可不等，则为变长指令字结构。

按操作码长度分类

定长操作码：指令系统中所有指令的操作码长度都相同。

可变长操作码：指令系统中各指令的操作码长度可变。

对于前者，若操作码有n为则指令种类有$2^n$，这种方式控制器的译码器电路设计相对简单，但灵活性低，后者则相反。

按操作类型分类

扩展操作码指令格式

扩展操作码指令格式采用定长指令字结构和可变长操作码。也就是说指令总长度是固定的，操作码在一定范围内长度是可变的。

若指令字长16位，每个地址码4位，三地址指令的前四位用于OP，后面跟3个4位长的地址段。4位基本操作码若全用于3地址指令，则有16条。如果还想设计二地址、一地址、零地址指令，至少必须将1111留作扩展操作码用，此时三地址指令总共15条。

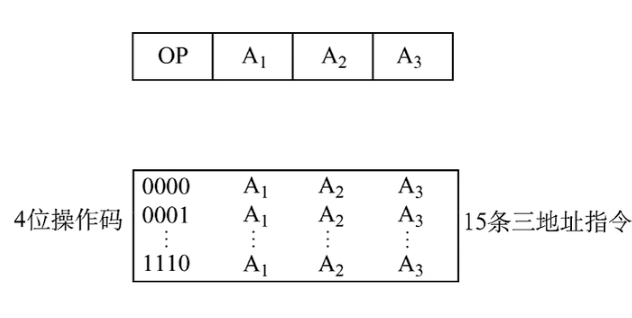
同样对于二地址指令，前4位全1，中间（原A1处）的4位范围只有0000到1110，是因为1111要留给一地址指令。

对于一地址指令，前8位全1，后面同理。

当然上述只是一种扩展方式，还有其他方式可以使用。

扩展时需要注意：

• 不允许短码是长码的前缀，即短操作码前面不能与长操作码前面部分相同
• 各指令的操作码一定不能重复

通常情况下，使用频率高的指令分配短操作码，频率低的分配长操作码，以此降低指令译码和分析的时间。

我们举一个例子：

指令寻址

顺序寻址

指令寻址依赖于程序计数器PC，下一条欲执行的指令始终由程序计数器给出。

我们假设系统采用定长指令字结构，并且指令字长与存储字长都是16Bit即2Byte ，主存按字编址。

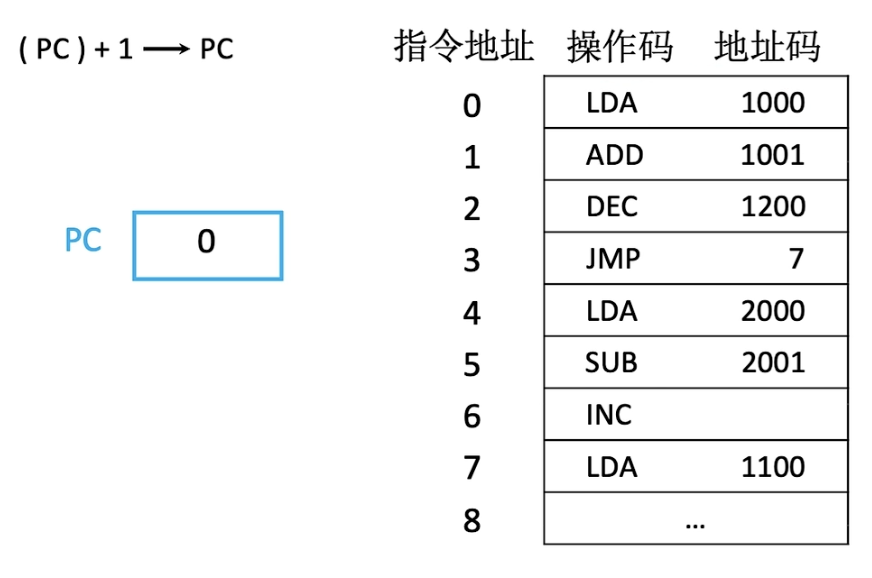
在一开始PC为0，随后取出地址为0的指令，此时PC+1，指向下一条指令。

这里需要注意，PC总是在取出当前地址指令后加1，指向下一条指令，而不是指向当前指令。

另外，对于PC加1的这个1实际上是单位1，应当理解为1个指令字长。如果主存是按字节编址，而不是按字编址，若指令字长为2字节的话，那么程序计数器应当加2，也就是对于程序计数器来讲，此时2字节算1个单位。

当然，系统不一定非要采用定长指令结构，还有可能是变长指令结构。

系统采用变长指令结构，并且指令字长和存储字长都是2Byte，主存按照字节编址。上图中同一种颜色的区块为一条指令。

此时CPU会读入一个字，根据操作码判断这条指令的总字节数n，然后修改PC的值。例如对于第一条指令，占两个字，即4个字节，CPU将第一个字也就是前两个字节取出，随后CPU再取出后两个字节，这样才完整取出一条指令。对于这条指令，n的大小为4，也就是说取指令完毕后PC计数器会加4.

对于第二条指令PC加2，第三条则加6，以此类推。

跳跃寻址

上述由PC计数器一直加“1”这种寻址方式叫做顺序寻址，与之对应的成为跳跃寻址。

我们看到上图中有一个汇编指令为JMP其含义为跳跃到地址为7的指令，这种方式就是一种跳跃寻址。当CPU取出这条指令后，PC仍然按照之前的规则加“1”，但是由于JMP指令的作用，PC随后会被改为7。

在计算机实际运行的过程中，同一时刻可能存在许多程序并发运行，所以地址码不一定从零开始。比如该程序的地址码从100开始，对于JMP 7这条指令，就不能按照以上方式直接跳转到7了，而是相对于100的偏移量。

数据寻址

对于地址码主要有10种寻址方式，通常会在前面标识4个比特位来区分是哪种方式。

在接下来的讲解过程中，我们都假设指令字长等于机器字长等于存储字长。并假设操作数为3。

直接寻址

直接寻址，也就是说指令字中的形式地址A就是操作数的真实地址EA。

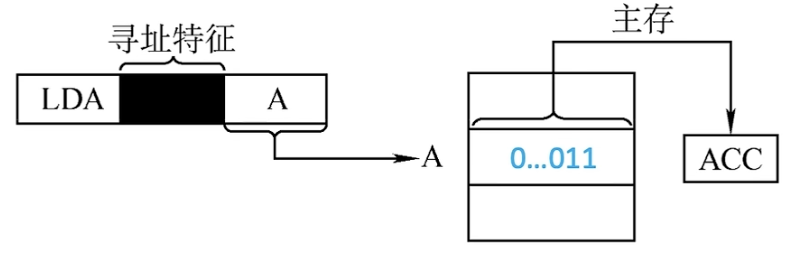
执行上图中的指令，取指令访存一次，执行指令访存一次，总共2次。

对于直接寻址，执行起来比较简单，指令执行阶段（注意不是整个寻址阶段）只需要访存1次，不需要专门计算操作数的地址。指令字中的地址A直接被送往MAR。

但是这种方式对于给出的地址的位数是有限的，假设指令总共32Bit，形式地址A的位数为16位，那么寻址范围只有0到$2^{16} - 1$

间接寻址

指令的地址字段给出的形式地址不是操作数的真正地址，而是操作数的有效地址所在存储单元的地址，也就是操作数地址的地址，即$EA = (A)$

对于上图中的指令，总共需要3次访存：取指令访存1次，执行指令访存2次。

对于执行指令的过程，需要通过EA来获取操作数的真实地址，然后再去访问操作数，因此相对于直接寻址多了1次。

当然间接寻址还可能不只一次，例如两次间接寻址，首先根据指令字保存的地址A找到对应的存储单元，若过该单元第一位数字为1，那么也就是说还需要进行间接寻址，然后根据该单元中的地址A1找到存放操作数真实地址的存储单元，这个单元的第一位应当是0表示无需再进行间接寻址，并且所存放的地址就是操作数的真实地址EA。最后根据EA找到存放操作数的存储单元即可。

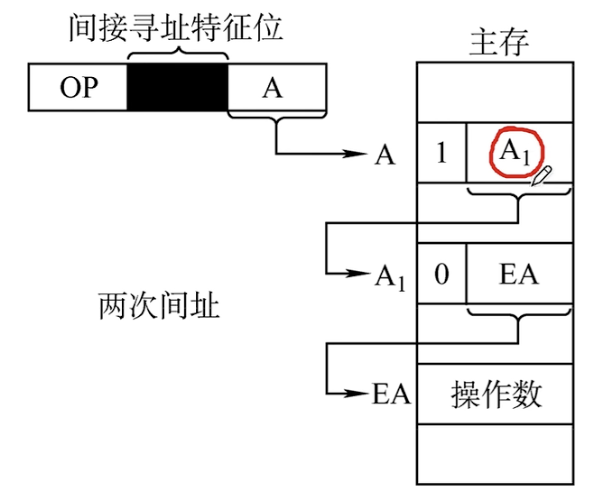
使用间接寻址的方式可以扩大寻址范围，即有效地址EA的位数大于形式地址A的位数。而且便于编制程序，使用间接寻址可以方便地完成子程序返回操作。

但是间接寻址要在执行阶段多次访存（一次间址两次访存），多次寻址需根据存储字的最高位确定几次访存。

寄存器寻址

在指令字中直接给出操作数所在的寄存器编号，即$EA = R_i$，操作数在由$R_i$所指的寄存器内。

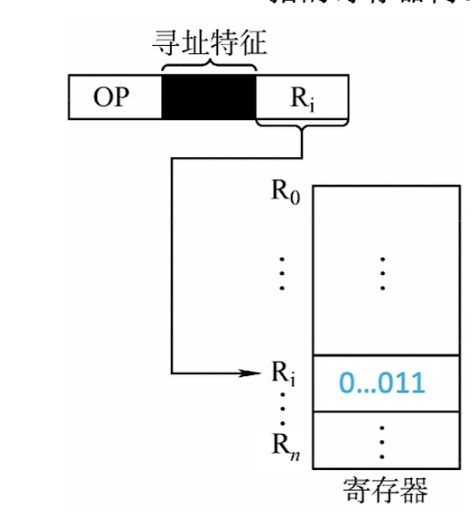
如图所示，取指令访存1次，执行指令访存0次，在不考虑存储结果的情况下总共访存1次。

其优点显而易见了，指令在执行阶段不访问主存，只访问寄存器，指令字短并且执行速度快，支持向量/矩阵运算。

缺点与寄存器有关，寄存器成本高且个数有限。

寄存器间接寻址

显然这就是综合了间接寻址和寄存器寻址两种方式。很明显寄存器中存储的不是操作数，而是操作数所在主存单元的地址。即$EA = (R_i)$

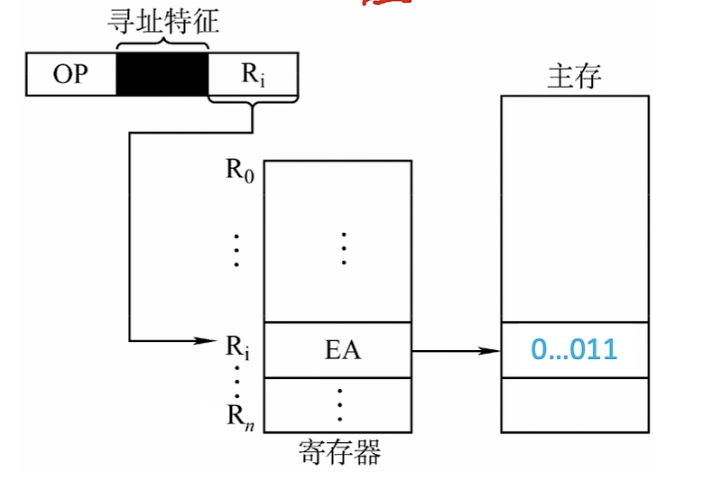
如图所示，取指令访存1次，执行指令访存1次、访问寄存器1次。总共访存2次。

这种寻址方式通常比一般的间接寻址方式要快，但相对于寄存器寻址，指令执行阶段需要访问主存。

隐含寻址

隐含寻址，顾名思义，不是明显地给出操作数的地址，而是在指令中隐含着操作数的地址。

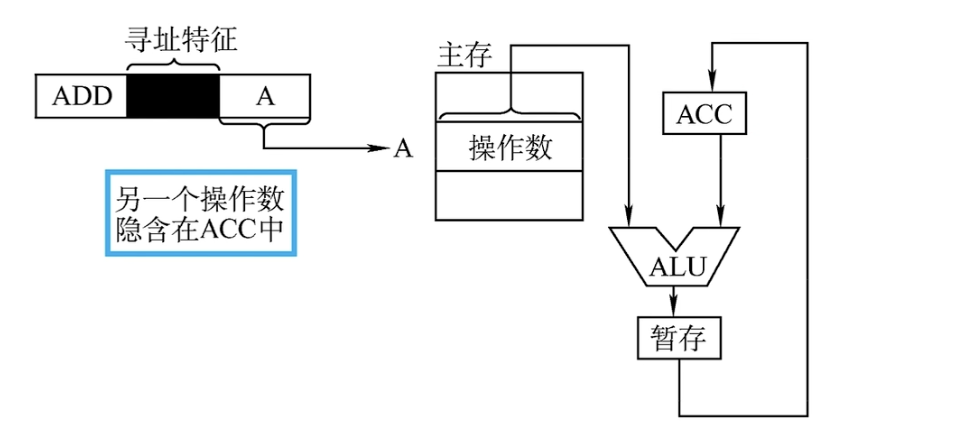
对于ADD指令，一个操作数通过访问主存或寄存器获取，另一个操作数隐含在ACC寄存器中。

• 优点：有利于缩短指令字长。
• 缺点：需增加存储操作数或隐含地址的硬件。

立即寻址

这种方式不同于直接寻址。指令字中存放的不是操作数的地址，而是操作数本身。这种操作数又被称为立即数，一般采用补码的形式。

在许多汇编语言中，如果指令后面跟一个井号开头的数字，例如LOAD #777，那么这个数字不是地址而是一个立即数。

对于这种方式，取指令访存1次，但是执行指令无需访存，如果不考虑存储结果，总共访存1次。

由于指令执行阶段不用访问主存，执行指令最短，但是位数限制了立即数的范围，如果A的位数位n，并且采用补码的形式，可表示的范围为$-2^{n-1}$到$2^{n-1}-1$。

偏移寻址

偏移寻址有三种方式：相对寻址、基址寻址、相对寻址。

基址寻址是以程序的存放地址为起点进行偏移，变址寻址由程序员自己决定哪里作为偏移的起始点，而相对寻址是以程序计数器作为偏移的起始点。

基址寻址

将CPU中的基址寄存器BR（有时也称重定位寄存器）的内容加上指令格式中的形式地址A，而形成操作数的有效地址，即$EA = (BR) + A$

除了采用专门的寄存器外，也可以使用通用寄存器来作为基地值寄存器。此时需要在指令中指明要将哪个通用寄存器作为基址寄存器使用，然后将寄存器的值与A通过ALU运算获取操作数的地址。

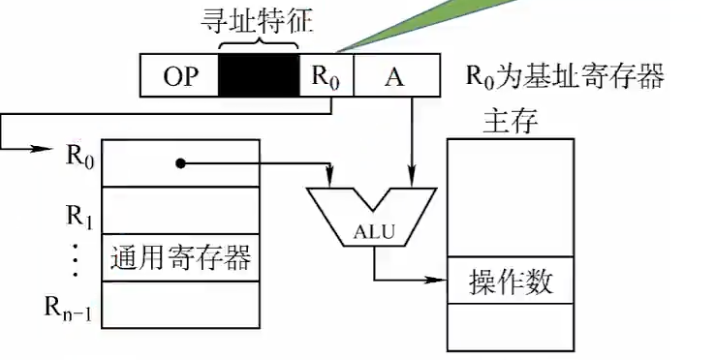
如上图所示，$R_0$所占的位数取决于通用寄存器的个数，如果通用寄存器有8个，那么$R_0$就要占3位。

基址寻址的意义在于方便程序“浮动”，方便实现多道程序并发运行。程序运行时，CPU都会将BR的值修改为该程序的起始地址（存放于OS的PCB中）。

BR是面向OS的，其内容由操作系统或者管理程序决定，在程序执行的过程，基址寄存器的内容不变，形式地址（作为偏移量）可变。也就是说程序员是不可以操作BR里的值的，程序放在什么位置是由OS决定的。

当采用通用寄存器作为基址寄存器的时候，可以由用户来决定哪个寄存器作为基址寄存器，但是其内容仍由OS确定。

变址寻址

对于变址寻址，有效地址EA等于指令字中的形式地址与变址寄存器IX的内容相加之和，即$EA = (IX) + A$，其中IX可以为专用的变址寄存器，也可以使用通用寄存器替代。

变址寻址是面向用户的，在程序执行过程中，变址寄存器的内容可以由用户改变，IX作为偏移量，形式地址A不变作为基地址，这一点跟基址寻址不同。

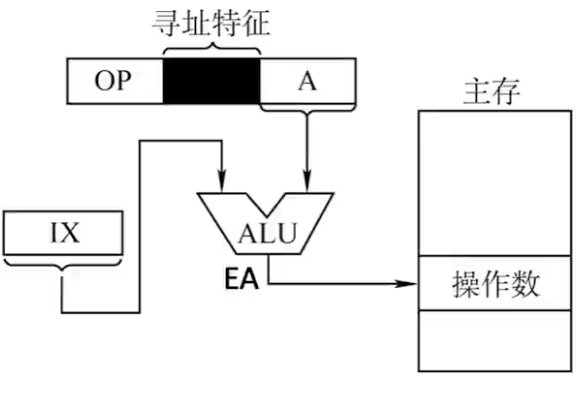
对于高级语言来讲，变址寻址通常用于循环、数组访问等，这提高了程序等灵活性。

我们来看一段C/C++语言的代码：

for(int i = 0; i < 10; i++){
  sum += a[i];
}

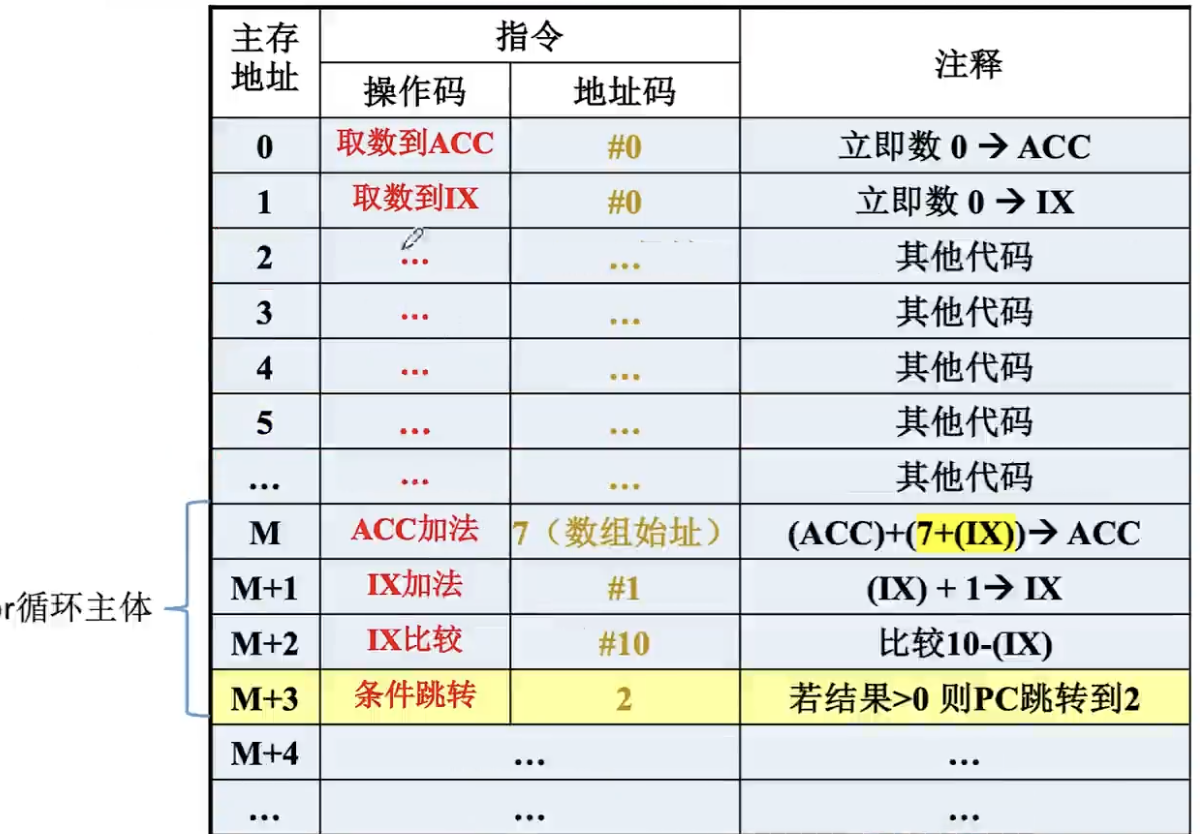
对于上述循环，我们假设数组元素个数只有10个，将每个元素一次累加到num。如果不采用IX的话对应的指令就应该如下：

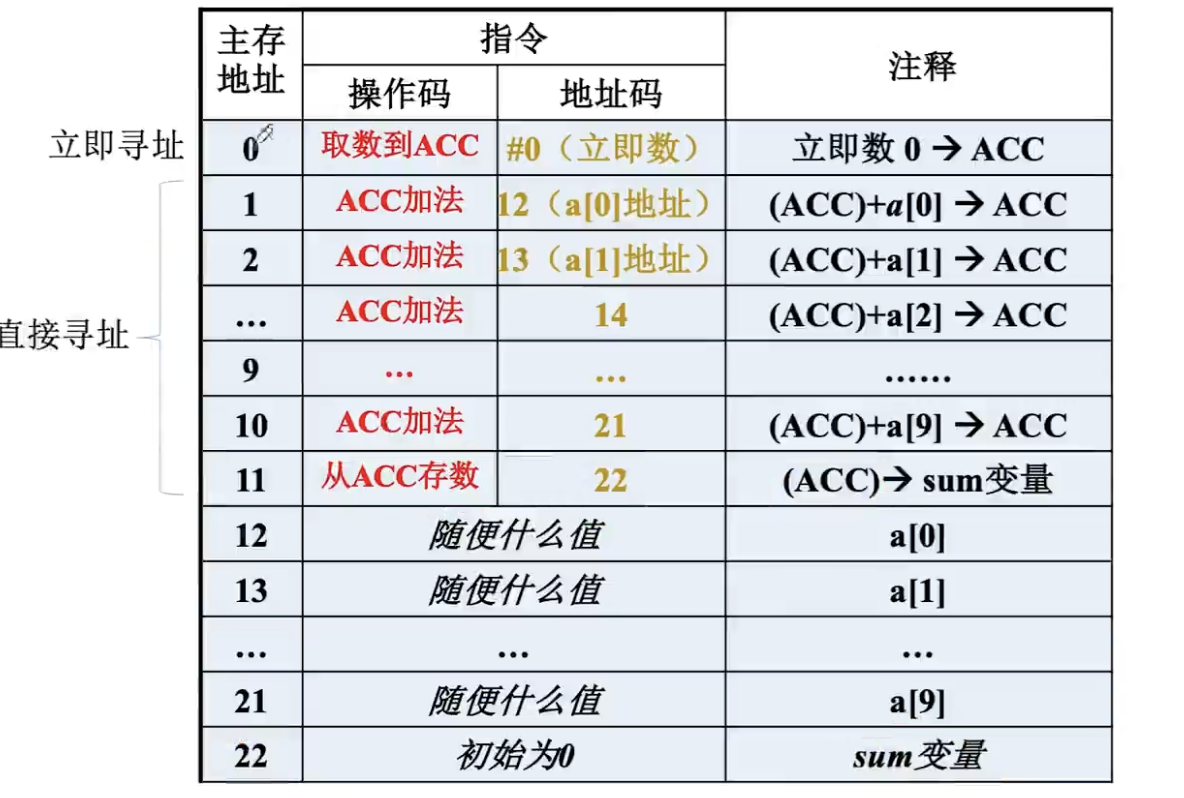
每一轮循环我们都要有对应的ACC加法指令，此时我们如果想改变数组大小，使其变为15个元素，那么就必须改变指令的个数，这对于编程来讲很不灵活。

当我们引入了IX后，就极大地方便了这一过程，如下图所示：

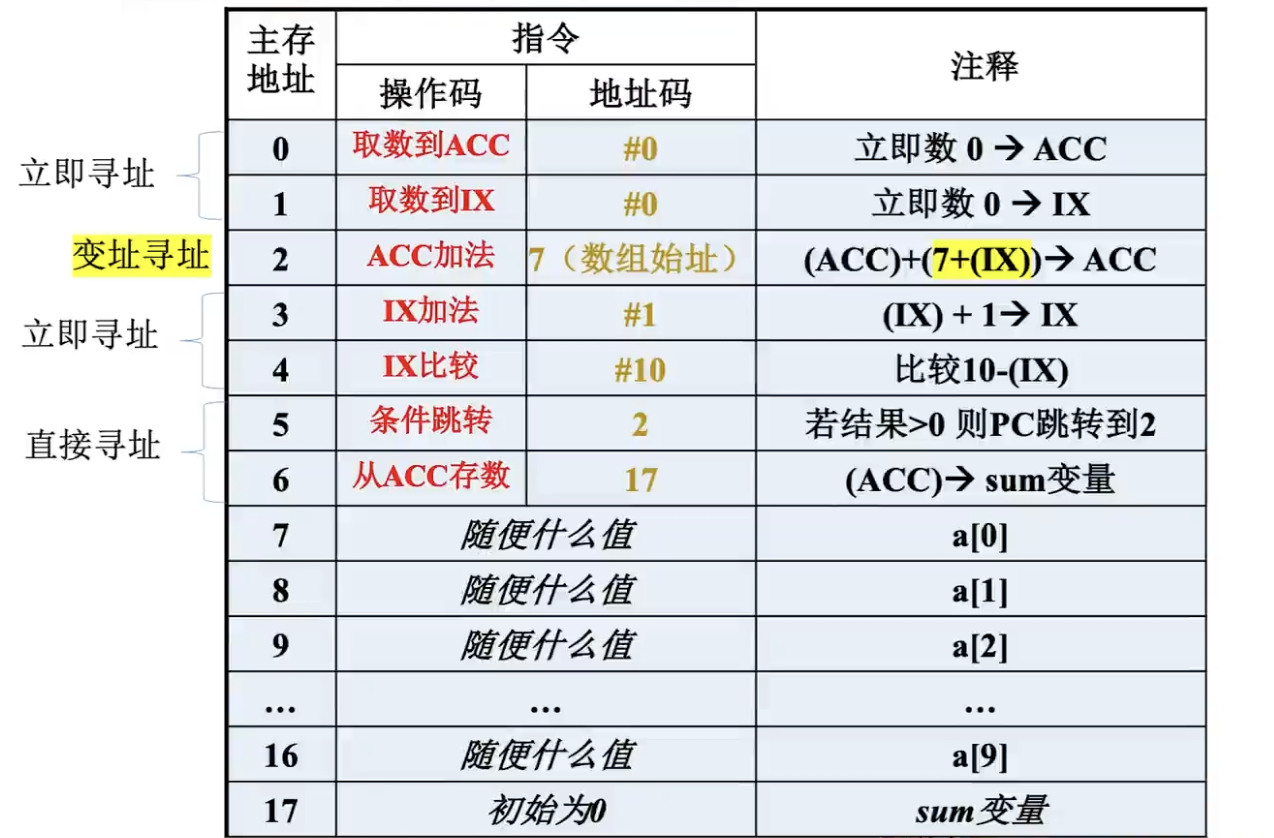
我们使用了一条比较指令来比较IX中的值与10哪个大（这里是通过做差的方式比较大小，此外，注意这里的10前面带有#，说明这是一个立即数，其储存在指令字中而不是主存中）。

如果比10小，那么条件跳转回2号指令。每次循环IX都被加1，依次偏移访问7之后的地址（7是数组始址，也就是0号元素存放的地址）所存储的数据，并累加到acc。循环结束后，将ACC的内容写入到sum。

由此可见不断改变IX的内容可以很容易地访问数组中任一数据的地址，特别适合编制循环程序。

基址&变址复合寻址

众所周知三大偏移寻址总共有4种（不是）

实际上这种只能算作两种寻址方式的复合，而没有单独拉出来分一类。

我们的程序初始地址不一定是从0开始，假设第一条指令地址为100，那么数组0号元素也就是107，这时候仅靠变址寻址就不行了，而是需要结合基址寻址，IX就成了偏移量的偏移量。

对于先基址再变址，公式为

$$ EA = (IX)+((BR) + A) $$

相对寻址

相对寻址：把程序计数器的内容加上指令格式中的形式地址A而形成操作数的有效地址。即

$$ EA = (PC) + A $$

与基址寻址区别在于，相对寻址是相对于程序计数器PC的，而基址寻址是相对于程序起始地址的。

上述公式中的A是相对于PC所指地址的偏移量，可以是正号也可以是负号，用补码表示。

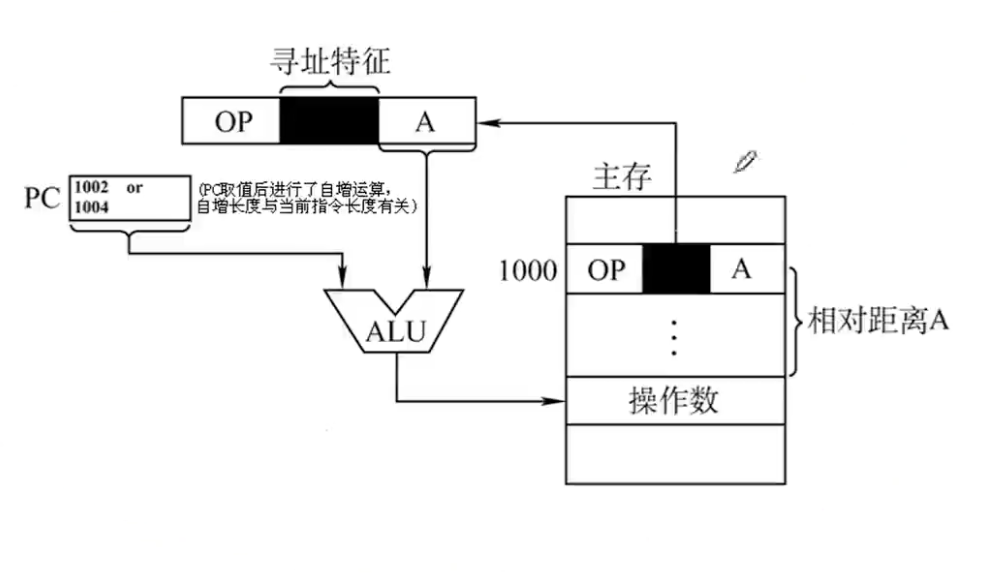
注意对于当前执行的指令，程序计数器PC永远指向下面一条指令，也就是说A是相对于下一条指令的偏移量。

我们还是来看这样一段代码:

for(int i = 0; i < 10; i++){
  sum += a[i];
}

在编写程序的时候，我们有可能调整代码逻辑，将这段代码放到其他地方。站在高级语言程序员的角度这没什么，但是从汇编角度来看，这种操作可能导致你的代码无法正常执行。我们假设其中有一个指令是条件跳转到2，如果这个片段被移动到其他位置，那么2这个地址就是不正确的。

因为2地址的指令也被移动到了其他位置。

如果再去修改相应的寻址方式的基地址或者偏移量，就会比较麻烦，极大地影响程序的灵活性。因此这时候就必须引入相对寻址。

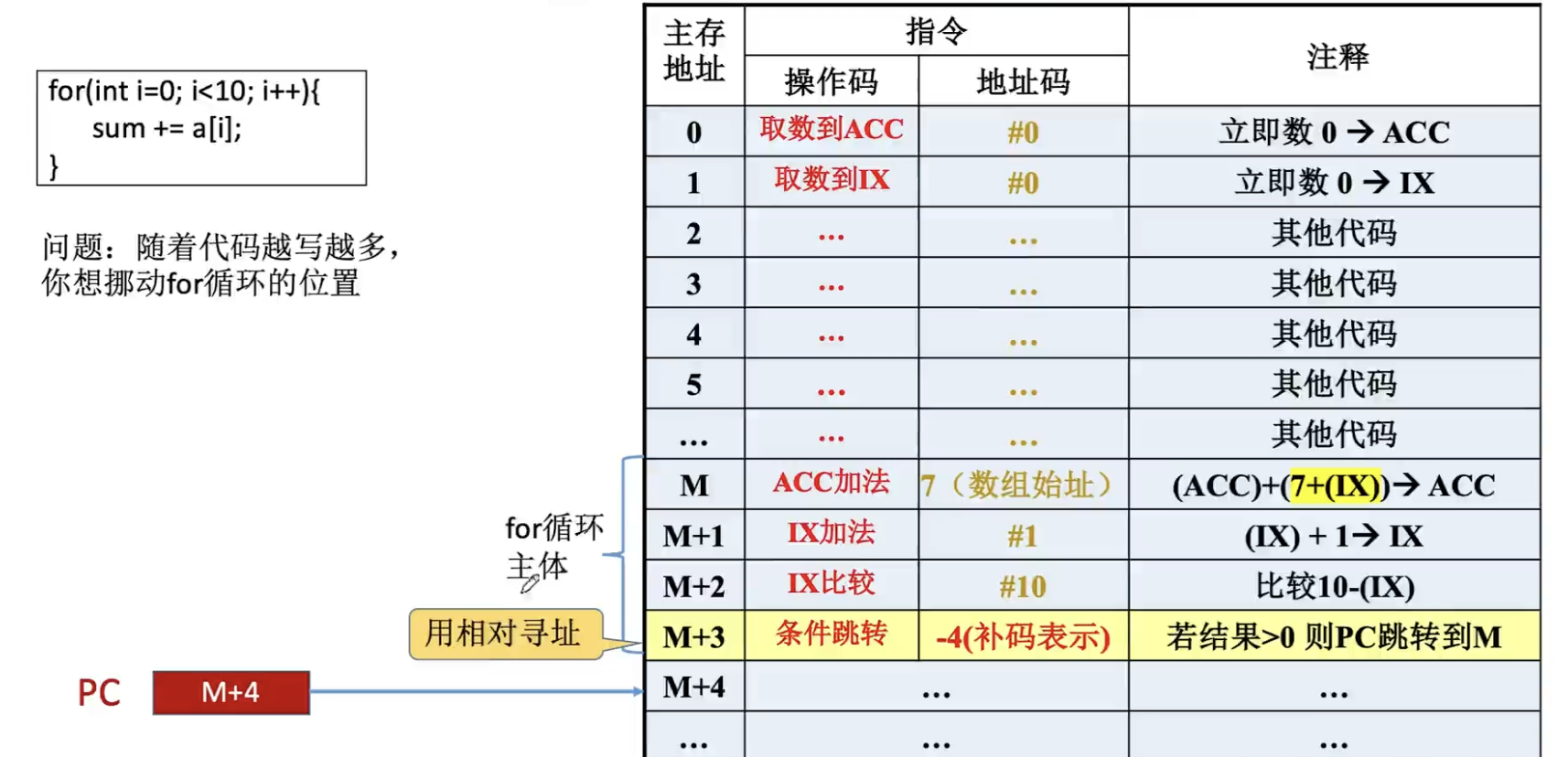
采用相对寻址，将偏移量修改为-4（补码表示，注意这里执行M+3的指令，偏移量是相对于PC此时也就是M+4的指令），程序自然而然就跳转了到了M处到指令。

另外对于M的ACC加法指令，其访问数组的位置也可能会发生变化，编写汇编程序的时候可以用分段的方式解决，即分为程序段、数据段。

相对寻址的优点在于，如果操作数地址不是固定的，它会随着PC的值变化而变化，并且与指令地址之间总是相差一个固定值，这时候采用相对寻址就有利于程序浮动（一段代码在整个程序内部浮动）。这种寻址方式广泛用于转移指令。

堆栈寻址

操作数存放在堆栈中，隐含使用堆栈指针SP作为操作数地址。堆栈是存储器或专用寄存器的存储区，该存储区中一块特定的按后进先出(LIFO)原则管理的存储区，该存储区中被读/写单元的地址是一个特定的寄存器给出的，该寄存器称为堆栈指针（SP）。

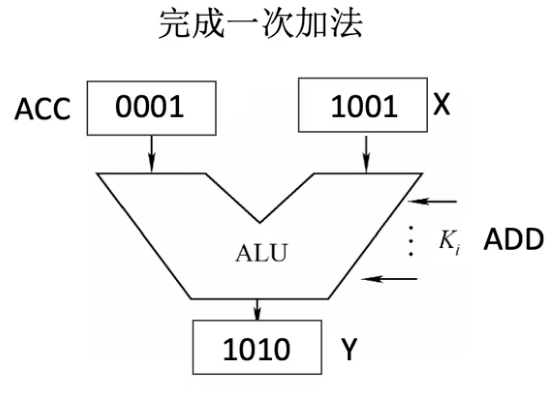
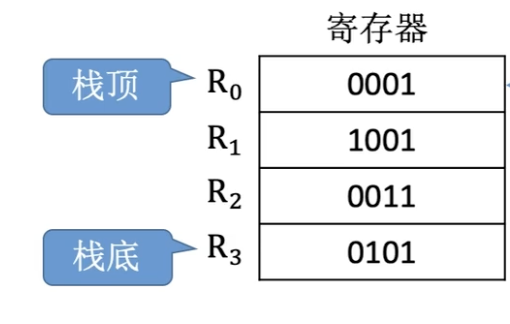
如图所示，堆栈寄存器首先把数据压入栈，然后SP指向栈顶，现在进行加法运算，从栈顶弹出第一个元素0001到ACC中，SP指向R1，再弹出第二个元素1001到寄存器X中，此时SP指向R2。经过ALU进行加法运算后，写入结果到一个通用寄存器Y，然后将Y中的内容1010压入栈顶，由于此时SP指向R2，所以元素存放的位置为R1，也就是说压入元素后SP就指向R1的位置。

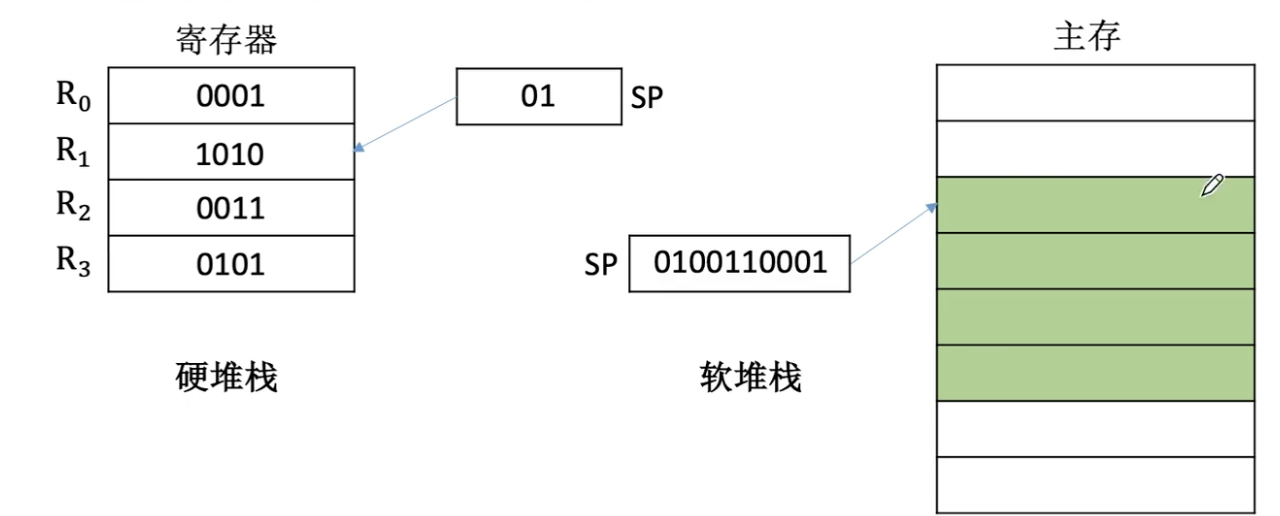
上图所有情况都是使用寄存器完成的，没有访问主存，所以这种方式叫做硬堆栈。与之对应的就是软堆栈，这种方式是通过软件在主存中分配一个堆栈，通过软件的方式指定堆栈的边界，SP指向的是主存的某块区域。

硬堆栈的方式成本比较高，软堆栈的方式成本相对较低。

总结