哈夫曼树及哈夫曼编码（基于优先队列实现）

概念

基础

• 路径：从树中一个结点到另一个结点之间的分支
• 路径长度：路径上的分支数目称为路径长度
• 树的路径长度：从树根到每一结点的路径长度之和
• 结点的带权路径长度：从该结点到树根之间的路径长度与结点上的权值的乘积
• 树的带权路径长度WPL：树中所有叶子节点的带权路径长度之和

哈夫曼树概念

由树的带权路径长度(WPL)定义可得到公式如下，其中$w_i$为叶子结点权值，$l_i$为叶子结点路径长度

$$ WPL(n) = \sum_{i=1}^{n} w_il_i $$

设有如下n个权值

$$ \{w_1,w_2,...,w_n\} $$

构造一棵有n个叶子节点的二叉树，每个叶子的权值为$w_i$

其中，WPL最小的二叉树就被称作哈夫曼树，也叫最优二叉树

也就是说哈夫曼树的WPL满足如下条件

$$ WPL_{Haffman} = WPL_{min}(n) $$

由此概念不难理解，哈夫曼树的形态不是唯一的，但是具有一组权值的各哈夫曼树的WPL是唯一的

从根节点出发，连接左儿子的边记为0，连接右儿子的边记为1，一直到叶子节点，所经过的边的编号构成的二进制序列即为该叶子结点的哈夫曼编码

哈夫曼编码的优点在于，对于每个叶子节点（对应唯一的字母或其他数据）的编码是唯一的，且任意一个编码不会是另外一个编码的前缀，这确保了解码的唯一性。

另外还有一些性质：

对于具有$n_0$个叶子结点的哈夫曼树，其结点数如下

$$ node = 2n_0-1 $$

构建哈夫曼树与获取哈夫曼编码

假设有这样四个字母与它们权值构成的序偶组成的集合如下

$$ \{(A,2),(B,5),(C,4),(D,9)\} $$

利用该数据构建哈夫曼树

首先将上述数据看成只有一个结点的二叉树

取出两个根节点权值最小的二叉树

$$ \{2，4\} $$

将两者（左子树根结点权值小于等于右子树根节点）连接到同一个父节点上，则其父节点的权值为6

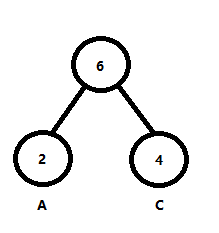
加上刚才诞生的新的树，还没有被利用的树的根节点对应的权值有

$$ \{5,6,9\} $$

同样再选出两个最小的（如果这时候，新构造的根节点与原有的根节点权值相等，则原有的根节点对应的树作为左子树，新构造的根节点对应的树作为右子树），重复上述步骤即可得到下图

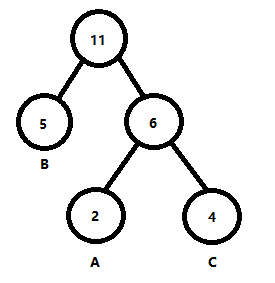
这时候只剩下两棵树没被使用，其根节点对应的权值如下

$$ \{9,11\} $$

同样再次执行上述步骤即可将所有树利用，即得到一个完整的哈夫曼树

将连接左儿子的边记为0，连接右儿子的边记为1

即可得到各个字母的哈夫曼编码

（我一般习惯将编码序列从右往左写，例如A的为011,，如果从左往右写就要写成110，本文包括下文中的代码演示均使用从右向左的方法）

$$ A:011,B:01,C:111,D:0 $$

如果一串字符串BDA则对应的哈夫曼编码如下（字符串顺序从左往右读，编码从右向左读取来解码）

$$ 0\space10\space011 $$

代码演示

类定义

首先定义一个哈夫曼树的类

typedef vector<pair<int, char>> huff;

class Huffman {
private:
    //结点定义
    class node {
    public:
        char word;
        int weight;                //权值

        node *lc, *rc;    //左儿子结点，右儿子结点
        string code;
        
        node(int weight, char word) {
            lc = nullptr;
            rc = nullptr;
            code = "";

            this->word = word;
            this->weight = weight;
        }
    };

private:
    priority_queue<pair<int, node*>, vector<pair<int, node*>>, greater<pair<int, node*>>> que;    //存放结点指针的优先队列（小根堆）
    node* root;    //根结点
    unordered_map<char, string> un_map;

public:
    Huffman(vector<pair<int, char>> vec);
    string Find(char index);

private:
    void _CreateCode(node *n, stack<string> st, int flag);

};

方法

构造函数

Huffman::Huffman(vector<pair<int,char>> vec)
{
    //将外部数据转成结点，存放到优先队列
    for (auto it = vec.begin(); it != vec.end(); it++)
    {
        node* p = new node(it->first, it->second);
        this->que.push(make_pair(it->first,p));
    }

    //构造哈夫曼树
    int cnt = 0;    //计数，每弹出两个结点连接到一个父节点，cnt置为0
    pair<int,node*> temp[2];
    while (!que.empty())
    {
        if (cnt >= 2)
        {
            node* p = new node(temp[0].first + temp[1].first, ' ');
            p->lc = temp[0].second;
            p->rc = temp[1].second;
            que.push(make_pair(temp[0].first + temp[1].first, p));
            cnt = 0;

            this->root = p;    //不断设置根节点
            continue;
        }

        temp[cnt] = que.top();
        que.pop();
        cnt++;
    }
    //最后会剩余两个结点于temp中，把它们连接起来
    node* p = new node(temp[0].first + temp[1].first, ' ');
    p->lc = temp[0].second;
    p->rc = temp[1].second;
    this->root = p;


    //建立叶子节点编码，左分支为0，右分支为1
    stack<string> st;
    _CreateCode(this->root, st, 0);

}

编码映射

将字母对应的哈夫曼编码保存到叶子节点中去，并且创建一个映射关系到map中

void Huffman::_CreateCode(node *n,stack<string> st, int flag)
{
    if (!n) return;

    flag == -1 ? st.push("0") : (flag == 0 ? st.push("") : st.push("1"));
    if (n->lc == nullptr && n->rc == nullptr)
    {
        while (!st.empty())
        {
            n->code += st.top();
            st.pop();
        }
        un_map[n->word] = n->code;
        return;
    }

    this->_CreateCode(n->lc, st, -1);
    this->_CreateCode(n->rc, st, 1);
}

查询

查询的话只需要返回unordered_map<char, string> un_map;相关的键对应的值就行了

string Huffman::Find(char index)
{
    return this->un_map[index];
}

结束

此处代码不足之处是还有解码没有实现。但是我觉得用每个字符的哈夫曼编码作为子串去匹配主串实现解码就行了，这应该是个字符串算法相关的问题，所以这里我就没写。